【Unity】マウスを円形に動かして値を増減させる

マウスカーソルを円形にくるくる動かして値を増減させてみます。

空のゲームオブジェクトにスクリプトを付けます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

public class WheelTestScript : MonoBehaviour
{
    [SerializeField] Text text;

    Vector2 mPos;
    Vector3 screenSizeHalf;
    float rad;
    float previousRad;
    float tan = 0f;

    // Start is called before the first frame update
    void Start()
    {
        // 画面の縦横の半分 
        screenSizeHalf.x = Screen.width / 2f;
        screenSizeHalf.y = Screen.height / 2f;
        screenSizeHalf.z = 0f;

        // マウスの初期位置
        mPos = Input.mousePosition - screenSizeHalf;
        previousRad = Mathf.Atan2(mPos.x, mPos.y);
    }

    // Update is called once per frame
    void Update()
    {
        // 真ん中が(0,0,0)になるようにマウスの位置を取得
        mPos = Input.mousePosition - screenSizeHalf;

        float rad = Mathf.Atan2(mPos.x, mPos.y); // 上向きとマウス位置のなす角
        float dRad = rad - previousRad; // 前のフレームの角度との差

        tan += Mathf.Tan(dRad); //タンジェント // * mPos.magnitude;
        text.text = tan + "";

        previousRad = rad; // 今のフレームの角度を保存
    }
}

Input.mousePositionで画面上のマウスカーソルの座標を取得すると、左下が(0,0,0)になるので、画面の縦横の幅の半分の値を引いて、画面の真ん中が(0,0,0)になるようにします。

// 画面の縦横の半分 
screenSizeHalf.x = Screen.width / 2f;
screenSizeHalf.y = Screen.height / 2f;
screenSizeHalf.z = 0f;

mPos = Input.mousePosition - screenSizeHalf;

そのxとyの値をMathf.Atan2に入れて、上方向と中心からカーソルへのベクトルのなす角を求めます。

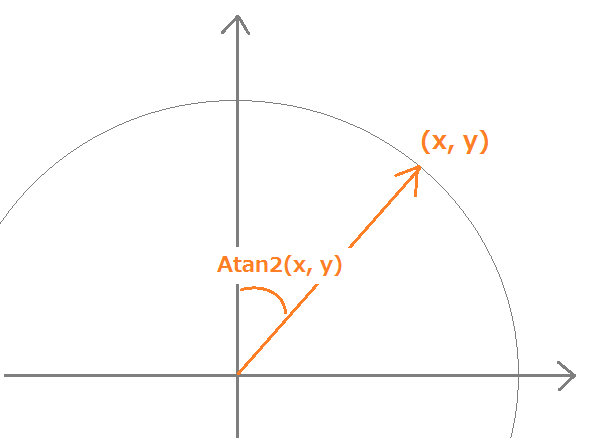
float rad = Mathf.Atan2(mPos.x, mPos.y);

これをUpdate()の最後に別の変数に保存しておくことで、前のフレームで求めた角度との差を計算できます。一番はじめのフレームでは、Start()で求めた角度を前のフレームの値として使っています。

float dRad = rad - previousRad;

// ---
previousRad = rad;

すると、今のフレームのマウスカーソルが前のフレームと比べて時計回りに回っていたらプラスの角度、反時計回りならマイナスの角度になります。

さらにその角度のタンジェントの値を求めて積み重ねていけば、時計回りにくるくる回すと増加して、反時計回りだと減少していく値が得られました。

tan += Mathf.Tan(dRad);

タンジェントにせずに角度のまま使うと、値が積み重なっていきません。

r += dRad;
text.text = r + "";

これは、Atan2で求める角度θが、-180度 < θ <= 180度 の範囲に制限されているからだと思います。

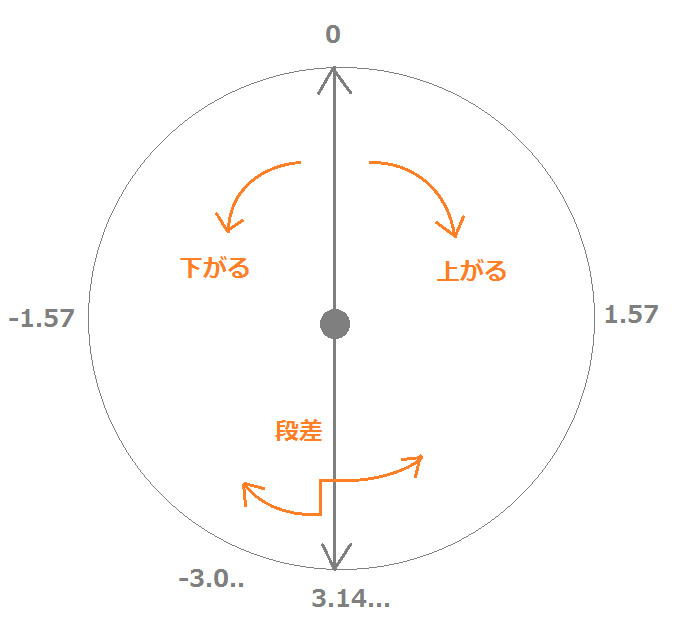
今と前のカーソル位置がこの段差によって別れたときは、角度の差の絶対値が大きな値になります。

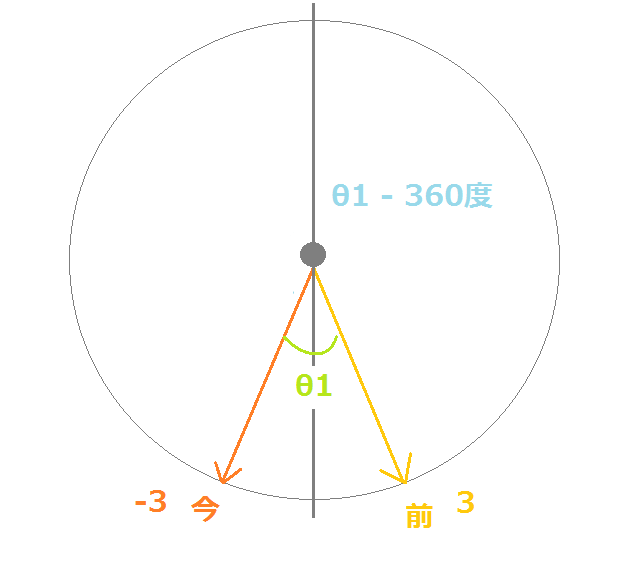
今の角度が -3 で前の角度が 3 のとき、今と前の差は -6 になります。これは、θ1ではなく、θ1 – 360度です。

今の角度をθ2、前の角度をθ3とすると、普段は θ1 = θ2 – θ3 と計算できます。

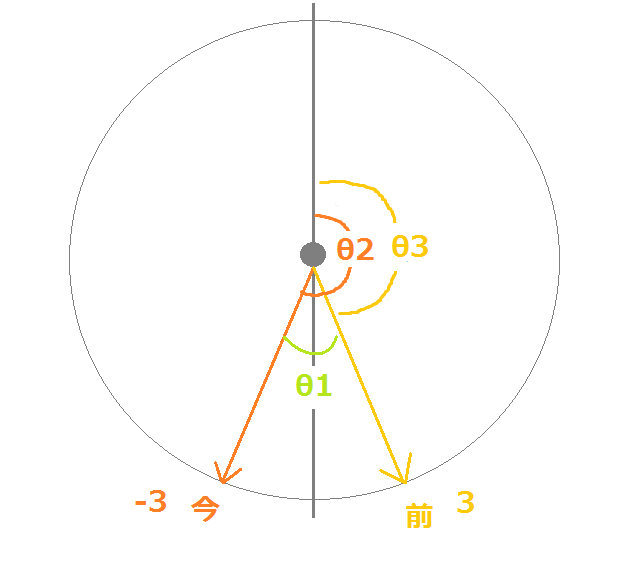
しかし、上のように今のカーソル位置だけが段差をまたぐと、θ2が -(360度 – θ2)に変わります。ここからθ3を引くと θ2 – θ3 – 360度 となって、絶対値の大きいマイナスの値になってしまい、増加していた値が一気に小さい値に戻ります。

しかしタンジェントθの値はθに360度の整数倍を足しても変わらないので、tan(θ2 – θ3 – 360度) = tan(θ2 – θ3)となって普段どおりの値が出ます。

なので、タンジェントにすると値が増加/減少し続ける値が得られるのではないかと思います。